MEMBRANE STUDIES
Our research team at the Netherlands Cancer Institute consisted, besides me, of senior biophysicist Willy S. Bont and our assistants Martha de Vries and Henny Hofs. We investigated the properties of membranes of rat liver cell nuclei using analytical ultracentrifugation (AUC). This research resulted in 1969 unexpectedly in the discovery of a discrete distribution pattern of reconstituted membrane vesicles in the size range of 30 to 600 μm diameter (Boom et al., 1976). The discreteness appeared to be regular, and could be mathematically formulated as a geometric series with a uniform ratio of approximately 21/2 for the mass, or surface area, of the vesicles. After many reruns and control experiments with membranes not only from other cell compartments and other species but also with artificial membranes (liposomes), we concluded that this pattern was reproducible and probably reflected a general physical property of membrane vesicles in vitro. For living cells this could be confirmed by comparison of the pattern with data from electron microscopic studies on the size of neurotransmitter and hormone vesicles in vivo (Bont et al., 1977).
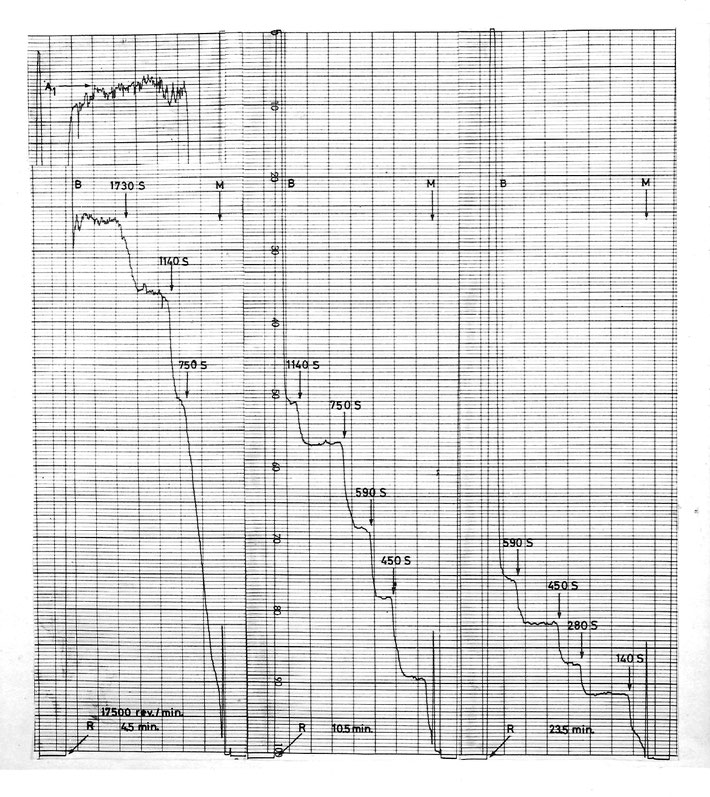
Characteristic discontinue sedimentation pattern of nuclear membrane vesicles in the analytical ultracentrifuge,
recorded Cby tracing the UV absorbance at successive time intervals
M = meniscus, B = bottom, calculated sedimentation coefficients in Svedberg units (Boom et al. 1976)
The sedimentation coefficients S are linearly proportional to the mass M of the vesicles, and the interpretation of these sedimentation patterns is a general correspondence between the vesicle masses and a geometrical series with a constant ratio of approximately 21/2. Because the main constituents of membranes are molecules (e.g. phospholipids, cholesterol) which organize themselves spontaneously in a closed globular surface layer, the vesicle mass is in turn proportional to the vesicle surface area (O), and, neglecting here a correction for the smallest vesicles, the correspondence becomes:
On = O1 . 2(n-1)/2
with the natural number n ranging from 1 to about 20 in our experiments.
In these series terms were regularly missing in the recording. Nuclear membranes, for example, were characterized by an alternating selection of terms, a series with mass ratio 2.
Schematical presentation of a vesicle series with mass (~ surface area) ratio 21/2 including an alternating series with ratio 2,
numbers correspond to the hypothetical order of a geometric series
Theoretical considerations - statistical mechanics of membranes as liquid crystals - resulted in a probabilistic interpretation of the distribution pattern of membrane vesicles. Instead of by the exact terms of a discrete geometric series, the distribution of vesicle fractions is now understood as the result of a wave function for the combined translation, rotation and vibration of the constituent molecules in the liquid crystal lattice. This complex wave function is unknown itself, but it is the reduced (or ‘collapsed’) form which is actually relevant for our observations. In its most simple form this can be formulated as a function of the probability density (p) of vesicles dependent on their size (e.g. diameter d) and the ratio r of the corresponding discrete series:
p ~ cos2[(2π / ln r2) x ln (d / dref.)]
We were able to show that this wave function is in fact a kind of ‘fingerprint’ for phenomena on any scale, ruled by membrane properties.
A revision of our last paper on this subject (Bont, 2009) is in preparation.
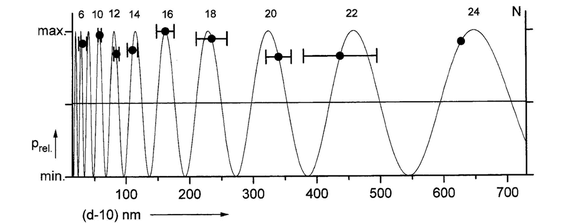
size distribution (diameters in nanometer units) of reconstituted nuclear membrane vesicles in vitro (Bont et al., 1977),
interpretation as 9 size classes with mass ratio 2 (~ diameter ratio 21/2).
Our results have been independently confirmed not only by comparable ultracentrifugation studies of rat intestinal plasma membranes in vitro (Walters et al., 1986) but also by electronmicroscopic studies of neurotransmitter vesicles in vivo in secretory cells of the mollusc Aplysia californica (Sossin et al., 1986 and Kreiner et al, 1986).
Moreover there has been an independent attempt to formulate a theoretical physical explanation for the quantum-like behavior of membranes reported by us (Sloot et al., 1993).
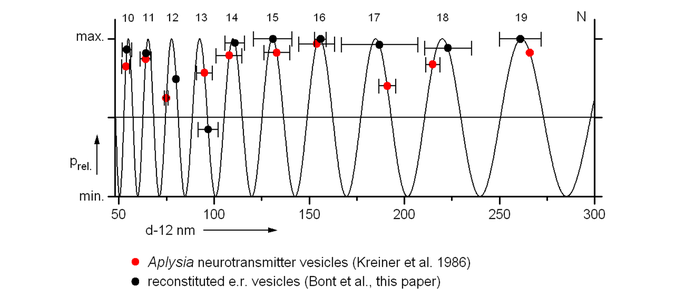
comparative analysis of the size distribution (diameters in nanometer units) of rat liver endoplasmatic reticulum membrane vesicles in vitro, and Aplysia neurotransmitter vesicles in vivo.probability density wave ratio: 21/4, bars: 95% confidence limits, numbers correspond to the hypothetical order of a geometrical series.
The characteristic quantum like distribution of isolated membrane structures ('fingerprint') can be traced back to many features of living things which are evidently ruled by membranes in their development and evolution. Here are four representative examples:
1. THE SIZE DISTRIBUTION OF FOSSIL MICROFOSSILS FROM THE EARLY PRE-CAMBRIUM
in relationship to the origin and early evolution of life on Earth and on Mars (Boom, 2012).
Polymodal size distribution of spheroid, alga-like microstrutures in sedimentary rocks of the Onverwacht Series (Swaziland System) in South Africa dated at more than 3.2 billion years BP, correlated positively with the membrane probability density wave. The proposition by the authors (Engel et al., 1968) that these lifelike forms are probably biological in origin is confirmed by the close correspondence. We have found 15 other reports of supposed spheroid life forms in the Pre-Cambrium, dating from 3.26 to 0.65 billion years BP likewise fitting in the membrane fingerprint.
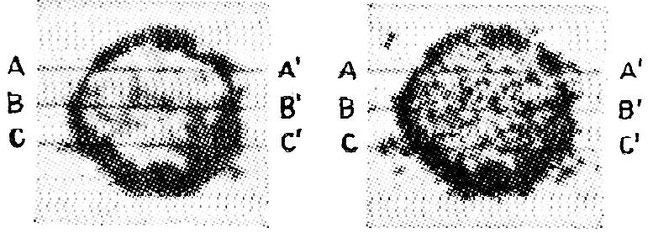
Two specimens of Archaeosphaeroides barbertonensis, the oldest record of life on earth, dated at more than 3.2 billion years BP, and probably close to the last universal common ancestor (LUCA) of all forms of life today. Size (B-B') ca 0.02 mm.
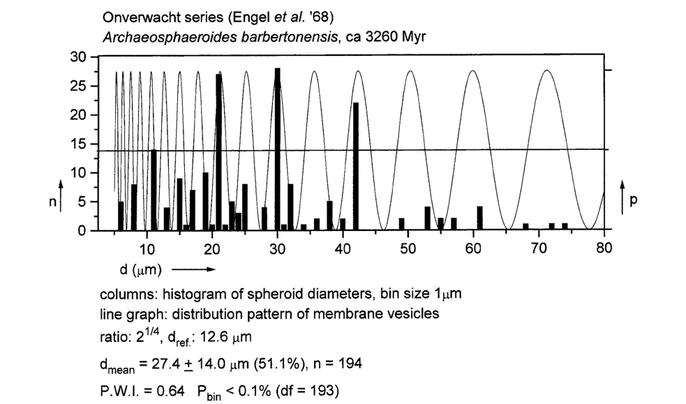
The result of our analyses support the hypothesis that self-organizing membranes played a major role in the origin and early evolution of life on earth.
A second paper is in preparation.
2. THE SIZE DISTRIBUTION OF SUCCESSIVE CHAMBERS IN FORAMINIFERA AND NAUTILIDAE
in relationship to their equiangular spiral architecture and evolution.
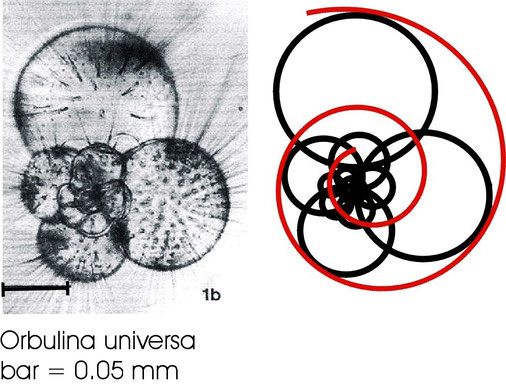
Microscopic image of a live specimen of the foraminifer Orbulina universa (Spero, 1988) showing an equiangular succesion of chambersin the micrometer size range
The mostly calcareous chamber walls of foraminiferal chambers are successively built on a membrane surface produced by the preceding chamber. The hypothesis being that they are in fact the fixations of membrane structures in live, as well as in dead and fossil specimens. Orbulina universa is a very common species present in all oceans. It has been selected because its chambers are almost perfectly globular and is therefore appropriate for measurements.

As shown above, the size distribution of successive chambers of one single specimen appears to fit very well with the membrane fingerprint. This was systematically confirmed by the results of measurements taken of several hundred shell specimens of two different species from the collection of the National Museum of Natural History, Naturalis, Leiden, The Netherlands. Our model for membranes as quantized liquid crystals, given appropriate constraints, also provides other possible discrete values of vesicle c.q. chamber ratio's. Consequently we were able to prove a similar correspondence with the membrane series in the chamber sequences of many other types of Foraminifera, the much bigger Nautilus pompilius and other extant and extinct cephalopods (e.g. Ammonites).
This could be the solution to the riddle of animal morphology that has bothered scientists for millennia (surveyed by D'A.W.Thompson in his 'On Growth and Form', 1942 and 1992).
A manuscript is in preparation.
3. THE SIZE DISTRIBUTION OF VERTEBRATE BRAINS
in relationship to the evolution of consciousness and intelligence.
Turning the attention from tiny isolated membrane vesicles in vitro to large brains of highly evolved species in vivo is a rather big jump that needs justification. The following arguments may help to understand the connection:
- membranes are a major and relatively constant component of brains from fish to mammals,
secondary only to proteins;
- inside the brain, the neurons, concentrated in the neocortex and responsible for the main brain
functions, are the principal contributors to the membrane content of the brain because they are per
cell uniquely equipped with thousands of extensions on a nanometer scale (dendrites and spines).
These form a complicated network interconnected by synapses all of which are without exception
enclosed in a membrane;
- there is growing support for the hypothesis that the neurons and their network of dendrites, probably
extended to the total neural system, actually behave as one coherent unit (see M.-W. Ho, 2008 for a
survey);
- that neural membranes are in fact the physical basis for this coherence is strongly supported by the
fact that their total surface area equipped with liquid crystalline properties, not unlike LCD screens,
is really huge (for human brains this is estimated at an amazing 2.5 ha, see Bear et al., 2001);
- the discovery of the first fossil remains of an evolutionary intermediary between the level of the great
apes and man, Pithecanthropus (now Homo) erectus in 1894 by the Dutch anatomist Eugene
Dubois produced the saltatory 'cephalization theory'. The initial support, subsequent rejection and
the now recent discussions of this Dubois conjecture triggered our interest in the evolutionary p
perspective because of its potential as a manifestation of our membrane model.
This information resulted in the working hypothesis that brain weight is correlated directly with the total neural membrane area. Therefore this parameter can probably be quantized too provided the membrane property is conserved in gradations from very small to very large scales.
The hypothesis was tested by statistical analysis using reliable data collections mainly provided by the zoological research groups of H. Stephan (Max Planck Institute for Brain Research, Frankfurt a.M.) and R. Bauchot (Universite Paris VII-Denis Diderot). We analyzed data collections of small brained (< 5gr.) animals, Insectivores, Prosimians, Bats and Birds with affirmative results. While Fish and Reptiles did not show a significant correlation with the membrane fingerprint.
The available data for large brained groups, Primates, Ungulates, Carnivores and Whales and Dolphins all showed a positive correlation, although, as expected, with a lower value for the probability wave ratio. As an example, a diagram of the analysis for the Primates (in logarithmized form) is shown below:
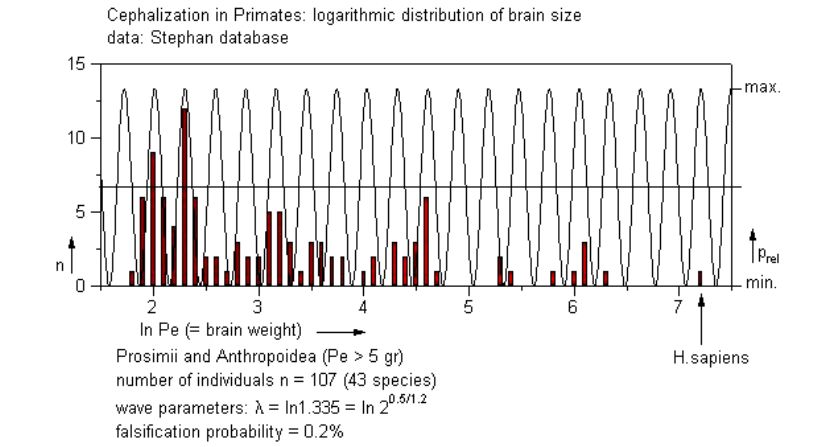
From our combined analyses we concluded that the quantumlike behavior of membranes is evidently indeed conserved from very small units (square micrometers) to very large ones (hectares). A range of many orders of magnitude, parts of which can be traced back to within the body of every living individual. They reflect the unmistakable saltatorial evolution of membrane-based morphological features of life from its origin about 3.5 billion years BP to the present day.
Brain size is also used for a provisional estimation of functional brain capacities at the level of individuals or species (e.g. the level of zoological intelligence or encephalization according to Jerison, 1973). For this purpose, and for obvious reasons, the absolute brain size (Pe) needs to be corrected to body size (Ps). The standard empirical allometric formula for relative brain size (k) is used:
k = Pe / Psa
Our analyses indicated that the distributions of relative brain weights of related animal assemblages evidently match the membrane fingerprint too. Although body weight (Ps) and the allometric exponent (a) show considerable variability at the species level.
Notwithstanding many uncertainties, comparison of relative brain weights can be elucidating, as is shown by the analysis of hominid data (black = extinct, red = extant):
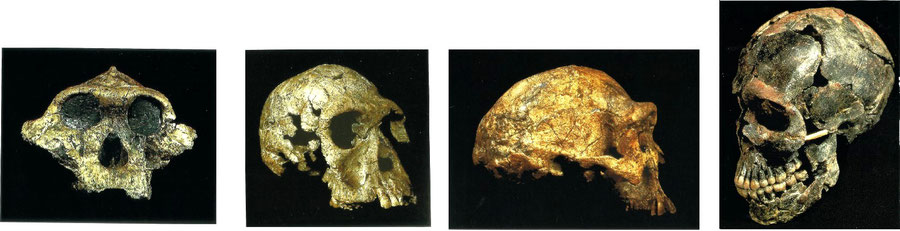
Australopithecus boisei (KNM-ER406) Homo habilis (KNM-ER1813) Homo erectus (KNM-ER3733) Homo sapiens (JQ 9)
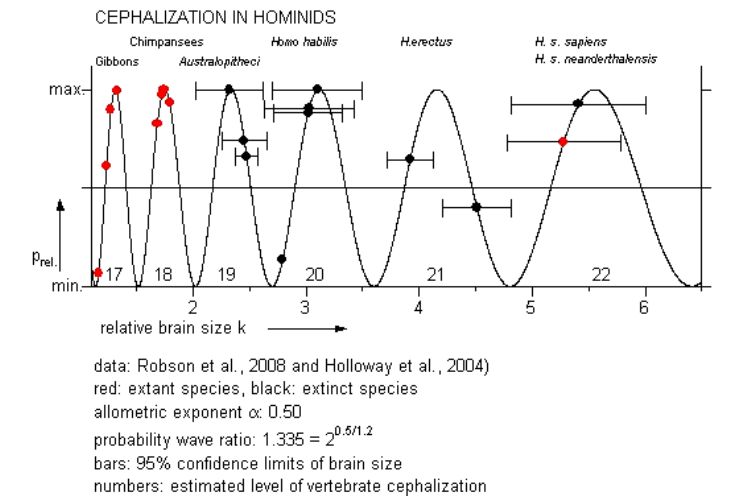
This result matches with the intuitive conception of a saltatory evolution of intelligence in the hominid succession. It also triggered the hypothesis that the neural membrane complex - with its immense and highly dynamic information potential - is the fundamental arena for the acts of consciousness.
The assemblage of Dolphins and Whales offers the only way to verify the distribution pattern at this level of cephalization. If we ignore the uncertainties of this comparison, the analysis does show a striking resemblance to that of the hominids, especially with all distinct levels occupied by living species and the Orca (Orcinus orca) possibly on the same level as Man.
A revision of a paper in first version ('On the Size of Vertebrate Brains', Boom et al., 1995) will be presented shortly.
4. CONSCIOUSNESS AND THE COSMOS
in relationship with quantumlike behavior at the galactic level.
While thinking about being conscious of an ordered cosmos as an idea born from consciousness .... the possibility came to mind that an order also could exist at the galactic level similar to that of membranes at the level of the brain. What I found is illustrated by the example below:
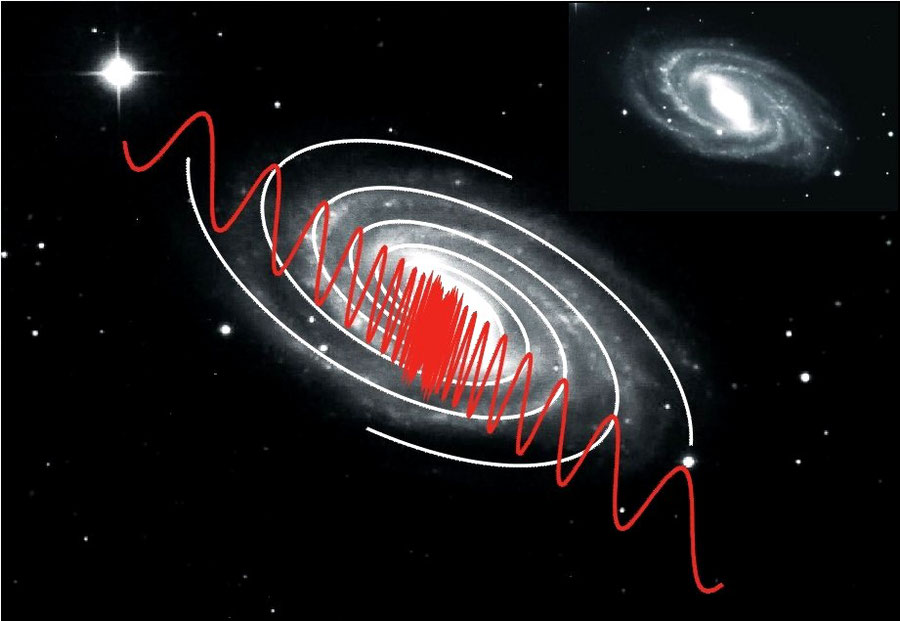
The four equiangular spiral arms of grand design galaxy NGC 3992 and the probability density wave which apparently governs their spacial distribution and is characterized by a ratio 21/2 of the successive radial vectors: an exact analogue of the membrane fingerprint.
Statistical analysis of data of more than 600 galactic spiral arms revealed a significant similarity of the radial density waves of stars to the, evidently analogue, probability density waves of membrane area's. My idea got wings. Just as neurons are depicted as the butterflies of the soul (Ramon y Cajal, 1904), galaxies seem to appear as the eagles of a cosmic mind.
A manuscript in first version on this subject is ready and will be prepared for publication shortly.
PRIMARY LITERATURE.
Boom,J., Bont, W.S. et al., Sedimentation Studies on Membrane Vesicles, Mol.Biol.Rep. 3, 81-86
(1976).
Bont, W.S., Boom, J. et al., Comparison between the Size of Granular Vesicles in Intact Cells and
Vesicles Obtained by Fragmentation of Biomembranes, J. Membrane Biol., 36, 213-232 (1977).
Walters, J.A.L.I. et al.. Membrane Vesicles of Cellullar Dimensions Fit in Two Geometric Series, J.
Membrane Biol., 91, 73-76 (1986).
Sossin, W., Kreiner, Th. And Scheller, R.H., Aplysia neurosecretory cells: multiple populations of
dense core vesicles, in: Fast and Slow Chemical Signalling in the Nervous System, Iversen L.L.
and Goodman, E.C. eds., Oxford University Press, Oxford (1986).
Sloot, P.M.A. et al., Crystallization on a sphere, 4th Int. Conf. Phys. Comp., 471-472 (1993).
Boom, J., Rotterdam, A. van, Bont, W.S., On the Size of Vertebrate Brains (1995), manuscript in
revision.
Bont, W.S., The basic property of biomembranes, Mol.Biol.Rep. 36(5), 959-964 (2009).
Boom, J., On the Search for Archetypal Life Forms, Lunar and Planetary Institute Contr. Series,
NASA- ID 4073 (2012).
Last update d.d. 10/08/2018

